How to Find General Solution of Trig Equations
6.1: Solving Trigonometric Equations
-
- Last updated
- Save as PDF
- Page ID
- 3342
An equation involving trigonometric functions is called a trigonometric equation. For example, an equation like
\[\nonumber
\tan\;A ~=~ 0.75 ~,
\]
which we encountered in Chapter 1, is a trigonometric equation. In Chapter 1 we were concerned only with finding a single solution (say, between \(0^\circ \) and \(90^\circ\)). In this section we will be concerned with finding the most general solution to such equations.
To see what that means, take the above equation \(\tan\;A = 0.75 \). Using the \(\fbox{\(\tan^{-1}\)}\) calculator button in degree mode, we get \(A=36.87^\circ \). However, we know that the tangent function has period \(\pi \) rad \(= 180^\circ \), i.e. it repeats every \(180^\circ \). Thus, there are many other possible answers for the value of \(A \), namely \(36.87^\circ + 180^\circ \), \(36.87^\circ - 180^\circ \), \(36.87^\circ + 360^\circ \), \(36.87^\circ - 360^\circ \), \(36.87^\circ + 540^\circ \), etc. We can write this in a more compact form:
\[\nonumber
A ~=~ 36.87^\circ \;+\; 180^\circ k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
This is the most general solution to the equation. Often the part that says "for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)'' is omitted since it is usually understood that \(k \) varies over all integers. The general solution in radians would be:
\[\nonumber
A ~=~ 0.6435 \;+\; \pi k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.1
Solve the equation \(\;2\,\sin\;\theta \;+\;1 ~=~ 0 \).
Solution:
Isolating \(\sin\;\theta \) gives \(\;\sin\;\theta ~=~ -\tfrac{1}{2} \). Using the \(\fbox{\(\sin^{-1}\)}\) calculator button in degree mode gives us \(\theta = -30^\circ \), which is in QIV. Recall that the reflection of this angle around the \(y\)-axis into QIII also has the same sine. That is, \(\sin\;210^\circ = -\tfrac{1}{2} \). Thus, since the sine function has period \(2\pi \) rad \(= 360^\circ \), and since \(-30^\circ \) does not differ from \(210^\circ \) by an integer multiple of \(360^\circ \), the general solution is:
\[\nonumber
\boxed{\theta ~=~ -30^\circ \;+\; 360^\circ k \quad\text{and}\quad 210^\circ \;+\;
360^\circ k} \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
In radians, the solution is:
\[\nonumber
\boxed{\theta ~=~ -\dfrac{\pi}{6} \;+\; 2\pi k \quad\text{and}\quad \dfrac{7\pi}{6} + 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
For the rest of this section we will write our solutions in radians.
Example 6.2
Solve the equation \(\;2\cos^2 \;\theta \;-\; 1 ~=~ 0 \).
Solution:
Isolating \(\;\cos^2 \;\theta \) gives us
\[\nonumber
\cos^2 \;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \pm\,\frac{1}{\sqrt{2}}
\quad\Rightarrow\quad \theta ~=~ \frac{\pi}{4}\;,~\frac{3\pi}{4}\;,~\frac{5\pi}{4}\;,~
\frac{7\pi}{4}~,
\]
and since the period of cosine is \(2\pi \), we would add \(2\pi k \) to each of those angles to get the general solution. But notice that the above angles differ by multiples of \(\frac{\pi}{2} \). So since every multiple of \(2\pi \) is also a multiple of \(\frac{\pi}{2} \), we can combine those four separate answers into one:
\[\nonumber
\boxed{\theta ~=~ \frac{\pi}{4} \;+\; \frac{\pi}{2}\,k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.3
Solve the equation \(\;2\,\sec\;\theta ~=~ 1 \).
Solution:
Isolating \(\;\sec\;\theta \) gives us
\[\nonumber
\sec\;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \frac{1}{\sec\;\theta} ~=~ 2~,
\]
which is impossible. Thus, there is \(\fbox{no solution}\).
Example 6.4
Solve the equation \(\;\cos\;\theta ~=~ \tan\;\theta \).
Solution:
The idea here is to use identities to put everything in terms of a single trigonometric function:
\[\nonumber \begin{align*}
\cos\;\theta ~&=~ \tan\;\theta\\ \nonumber
\cos\;\theta ~&=~ \frac{\sin\;\theta}{\cos\;\theta}\\ \nonumber
\cos^2 \;\theta ~&=~ \sin\;\theta\\ \nonumber
1 \;-\; \sin^2 \;\theta ~&=~ \sin\;\theta\\ \nonumber
0 ~&=~ \sin^2 \;\theta \;+\; \sin\;\theta \;-\; 1
\end{align*}\]
The last equation looks more complicated than the original equation, but notice that it is actually a quadratic equation: making the substitution \(x=\sin\;\theta \), we have
\[\nonumber
x^2 \;+\; x \;-\; 1 ~=~ 0 \quad\Rightarrow\quad x ~=~ \frac{-1 \;\pm\; \sqrt{1 - (4)\,(-1)}}{
2\,(1)} ~=~ \frac{-1 \;\pm\; \sqrt{5}}{2} ~=~ -1.618\;,~0.618
\]
by the quadratic formula from elementary algebra. But \(-1.618 < -1 \), so it is impossible that \(\;\sin\theta = x = -1.618 \). Thus, we must have \(\;\sin\;\theta = x = 0.618 \). Hence, there are two possible solutions: \(\theta = 0.666 \) rad in QI and its reflection \(\pi - \theta = 2.475\) rad around the \(y\)-axis in QII. Adding multiples of \(2\pi \) to these gives us the general solution:
\[\nonumber
\boxed{\theta ~=~ 0.666 \;+\; 2\pi k \quad\text{and}\quad 2.475 \;+\; 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.5
Solve the equation \(\;\sin\;\theta ~=~ \tan\;\theta \).
Solution:
Trying the same method as in the previous example, we get
\[\nonumber \begin{align*}
\sin\;\theta ~&=~ \tan\;\theta\\ \nonumber
\sin\;\theta ~&=~ \frac{\sin\;\theta}{\cos\;\theta}\\ \nonumber
\sin\;\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~\cos\;\theta \;-\; \sin\;\theta ~&=~ 0\\ \nonumber
\sin\;\theta~(\cos\;\theta \;-\; 1) ~&=~ 0\\ \nonumber
&\Rightarrow\quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ 1\\ \nonumber
&\Rightarrow\quad \theta ~=~ 0\;,~\pi \quad\text{or}\quad \theta ~=~ 0\\ \nonumber
&\Rightarrow\quad \theta ~=~ 0\;,~\pi~,
\end{align*}\]
plus multiples of \(2\pi \). So since the above angles are multiples of \(\pi \), and every multiple of \(2\pi \) is a multiple of \(\pi \), we can combine the two answers into one for the general solution:
\[\nonumber
\boxed{\theta ~=~ \pi k} \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.6
Solve the equation \(\;\cos\;3\theta ~=~ \frac{1}{2} \).
Solution:
The idea here is to solve for \(3\theta \) first, using the most general solution, and then divide that solution by \(3 \). So since \(\;\cos^{-1} \frac{1}{2} = \frac{\pi}{3} \), there are two possible solutions for \(3\theta\): \(3\theta = \frac{\pi}{3} \) in QI and its reflection \(-3\theta = -\frac{\pi}{3} \) around the \(x\)-axis in QIV. Adding multiples of \(2\pi \) to these gives us:
\[\nonumber
3\theta ~=~ \pm\,\frac{\pi}{3} \;+\; 2\pi k \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
So dividing everything by \(3 \) we get the general solution for \(\theta\):
\[\nonumber
\boxed{\theta ~=~ \pm\,\frac{\pi}{9} \;+\; \frac{2\pi}{3} k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.7
Solve the equation \(\;\sin\;2\theta ~=~ \sin\;\theta \).
Solution:
Here we use the double-angle formula for sine:
\[\nonumber \begin{align*}
\sin\;2\theta ~&=~ \sin\;\theta\\ \nonumber
2\,\sin\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~(2\,\cos\;\theta \;-\; 1) ~&=~ 0\\ \nonumber
&\Rightarrow\quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ \frac{1}{2}\\ \nonumber
&\Rightarrow\quad \theta ~=~ 0\;,~\pi \quad\text{or}\quad \theta ~=~ \pm\,\frac{\pi}{3}\\ \nonumber
&\Rightarrow\quad \boxed{\theta ~=~ \pi k \quad\text{and}\quad \pm\,\frac{\pi}{3} \;+\; 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\end{align*}
\]
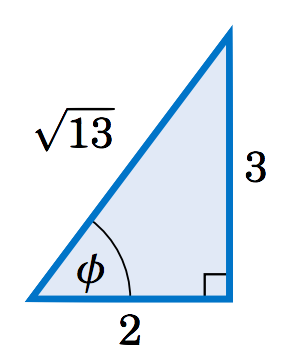
Solution:
We will use the technique which we discussed in Chapter 5 for finding the amplitude of a combination of sine and cosine functions. Take the coefficients \(2 \) and \(3 \) of \(\;\sin\;\theta \) and \(\;-\cos\;\theta \), respectively, in the above equation and make them the legs of a right triangle, as in Figure 6.1.1. Let \(\phi \) be the angle shown in the right triangle. The leg with length \(3 >0 \) means that the angle \(\phi \) is above the \(x\)-axis, and the leg with length \(2>0 \) means that \(\phi \) is to the right of the \(y\)-axis. Hence, \(\phi \) must be in QI. The hypotenuse has length \(\sqrt{13} \) by the Pythagorean Theorem, and hence \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) and \(\;\sin\;\theta = \frac{3}{\sqrt{13}} \). We can use this to transform the equation to solve as follows:
\[\nonumber \begin{align*}
2\,\sin\;\theta \;-\; 3\,\cos\;\theta ~&=~ 1\\ \nonumber
\sqrt{13}\,\left( \tfrac{2}{\sqrt{13}}\,\sin\;\theta \;-\; \tfrac{3}{\sqrt{13}}\,\cos\;\theta
\right) ~&=~ 1\\ \nonumber
\sqrt{13}\,( \cos\;\phi\;\sin\;\theta \;-\; \sin\;\phi\;\cos\;\theta ) ~&=~ 1\\ \nonumber
\sqrt{13}\,\sin\;(\theta - \phi) ~&=~ 1\quad\text{(by the sine subtraction formula)}\\ \nonumber
\sin\;(\theta - \phi) ~&=~ \tfrac{1}{\sqrt{13}}\\ \nonumber
&\Rightarrow\quad \theta - \phi ~=~ 0.281 \quad\text{or}\quad \theta - \phi ~=~ \pi - 0.281 = 2.861\\ \nonumber
&\Rightarrow\quad \theta ~=~ \phi \;+\; 0.281 \quad\text{or}\quad \theta ~=~ \phi \;+\; 2.861
\end{align*}\]
Now, since \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) and \(\phi \) is in QI, the most general solution for \(\phi \) is \(\phi = 0.983 + 2\pi k \) for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(... \). So since we needed to add multiples of \(2\pi \) to the solutions \(0.281 \) and \(2.861 \) anyway, the most general solution for \(\theta \) is:
\[\begin{align*}
\theta ~&=~ 0.983 \;+\; 0.281 \;+\; 2\pi k\quad\text{and}\quad 0.983 \;+\; 2.861 \;+\; 2\pi k\\
&\Rightarrow\quad \boxed{\theta ~=~ 1.264 \;+\; 2\pi k\quad\text{and}\quad 3.844 \;+\; 2\pi k}
\quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\end{align*}\]
Note: In Example 6.8 if the equation had been \(\;2\,\sin\;\theta \;+\; 3\,\cos\;\theta ~=~ 1 \) then we still would have used a right triangle with legs of lengths \(2 \) and \(3 \), but we would have used the sine addition formula instead of the subtraction formula.
How to Find General Solution of Trig Equations
Source: https://math.libretexts.org/Bookshelves/Precalculus/Book%3A_Elementary_Trigonometry_(Corral)/06%3A_Additional_Topics/6.01%3A_Solving_Trigonometric_Equations